https://www.acmicpc.net/problem/1932
1932번: 정수 삼각형
첫째 줄에 삼각형의 크기 n(1 ≤ n ≤ 500)이 주어지고, 둘째 줄부터 n+1번째 줄까지 정수 삼각형이 주어진다.
www.acmicpc.net
풀이
맨 위층부터 시작해서 아래에 있는 수 중 하나를 선택하여 아래층으로 내려올 때, 이제까지 선택된 수의 합이 최대가 되는 경로에 있는 수의 합을 구해야 한다.
아래층으로 내려올 때, 아래층에 있는 수에서 위층의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다. 즉, 현재 위치를 기준으로 위층의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중 최댓값을 선택하여 그 수와 현재 위치의 수를 더한 값을 현재 위치의 배열에 저장하면 된다.
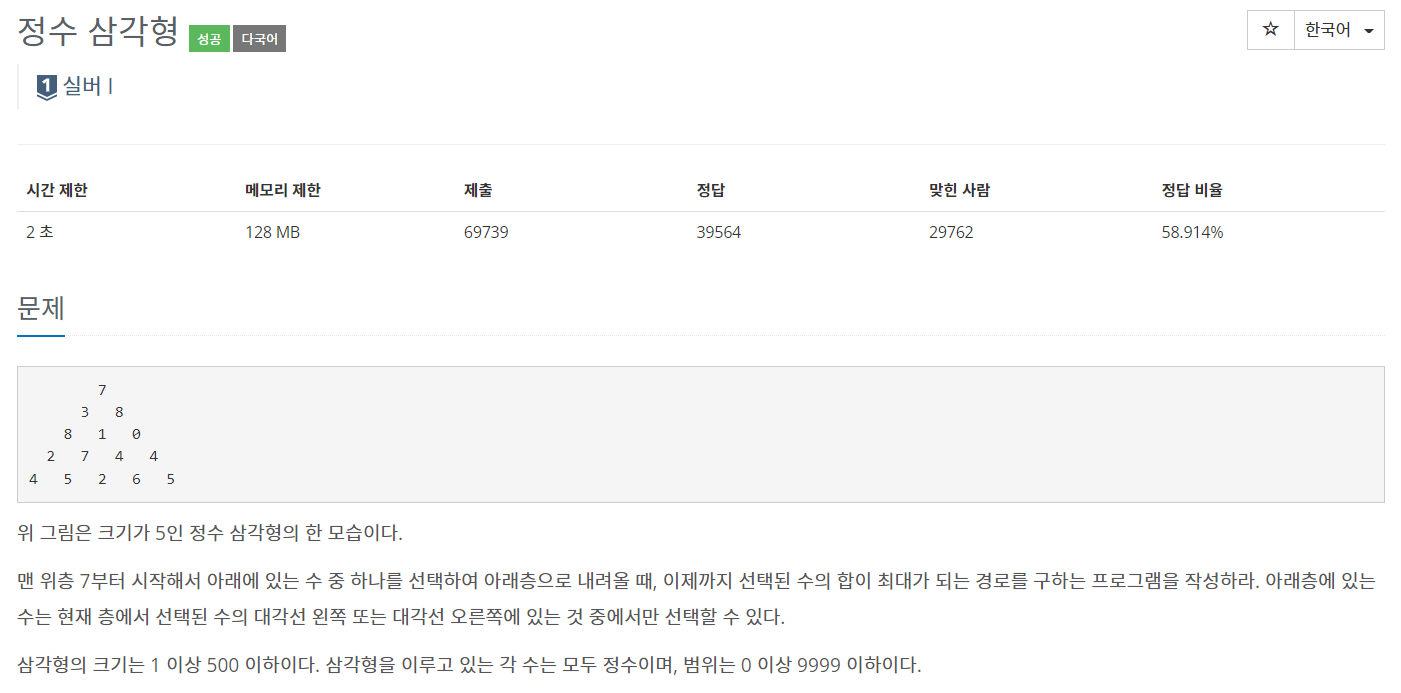
예시)
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
위와 같이 입력받은 정수 삼각형을 2차원 배열에 저장할 때 아래와 같이 로직을 수행한 다음 2차원 배열에 저장한다.
7
10 15
18 16 15
20 25 20 19
29 30 27 26 24
그 다음 맨 아래층에 있는 수들 중 최댓값을 출력한다.
정수 삼각형을 저장할 2차원 배열을 선언할 때 크기는 (n+1) x (n+1) 만큼 할당해야 한다. 크기를 (n+1) x (n+1) 만큼 할당하는 이유는 입력받는 정수 삼각형을 (1,1)에서부터 시작하여 위층의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중 최대값을 선택할 때, (1,1)의 경우 각각 위층의 (0,0), (0,1) 중 최대값을 선택할 수 있게 하기 위함이다. 자바에서는 int 배열을 선언하면 0으로 자동으로 초기화되기 때문에 위와 같은 방법이 가능하다.
로직
1. 삼각형의 크기 n을 입력받는다.
2. int형 2차원 배열 arr을 선언하고 크기는 (n+1) x (n+1) 만큼 할당한다.
3. arr[1][1]부터 시작하여 정수 삼각형을 입력받는다. 이 때 위층의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중 최대값을 선택하여 그 수와 입력받은 현재 위치의 수를 더한 값을 현재 위치의 배열에 저장한다.
4. 마지막 줄에 있는 수들 중 최댓값을 출력한다.
코드
import java.io.*;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[][] arr = new int[n+1][n+1];
StringTokenizer st;
//(1,1) 부터 정수 삼각형 시작
for (int i = 1; i <= n; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= i; j++) {
//위층의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중 최대값을 선택
arr[i][j] = Math.max(arr[i-1][j-1], arr[i-1][j]);
//선택한 최대값과 현재 위치의 정수를 더한 값을 현재 위치의 배열에 저장
arr[i][j] += Integer.parseInt(st.nextToken());;
}
}
int answer = 0;
//마지막 줄에 있는 수들 중 최댓값 출력
for (int j = 1; j <= n; j++) {
answer = Math.max(answer, arr[n][j]);
}
System.out.println(answer);
}
}
다른 풀이 2
첫번째 풀이는 위에서 아래로 내려가며 최댓값을 구했다. 반대로 아래에서 위로가며 최댓값을 구하는 방식도 가능하다.
이 때는 arr[0][0]의 값이 답이 된다.
import java.io.*;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
int[][] arr = new int[n][n];
StringTokenizer st;
for (int i = 0; i < n; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j <= i; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());;
}
}
for (int i = n-2; i>=0; i--) {
for (int j = 0; j <= i; j++) {
arr[i][j] = arr[i][j] + Math.max(arr[i+1][j], arr[i+1][j+1]);
}
}
System.out.println(arr[0][0]);
}
}
참고 : https://girawhale.tistory.com/52

'Algorithm 문제 풀이 > 백준' 카테고리의 다른 글
| [백준] 2630번 : 색종이 만들기 - 자바[Java] (0) | 2022.11.17 |
|---|---|
| [백준] 9184번 : 신나는 함수 실행 - 자바[Java] (0) | 2022.10.25 |
| [백준] 14503번 : 로봇 청소기 - 자바[Java] (0) | 2022.10.17 |
| [백준] 14501번 : 퇴사 - 자바[Java] (0) | 2022.10.16 |
| [백준] 1969번 : DNA - 자바[Java] (0) | 2022.10.09 |
