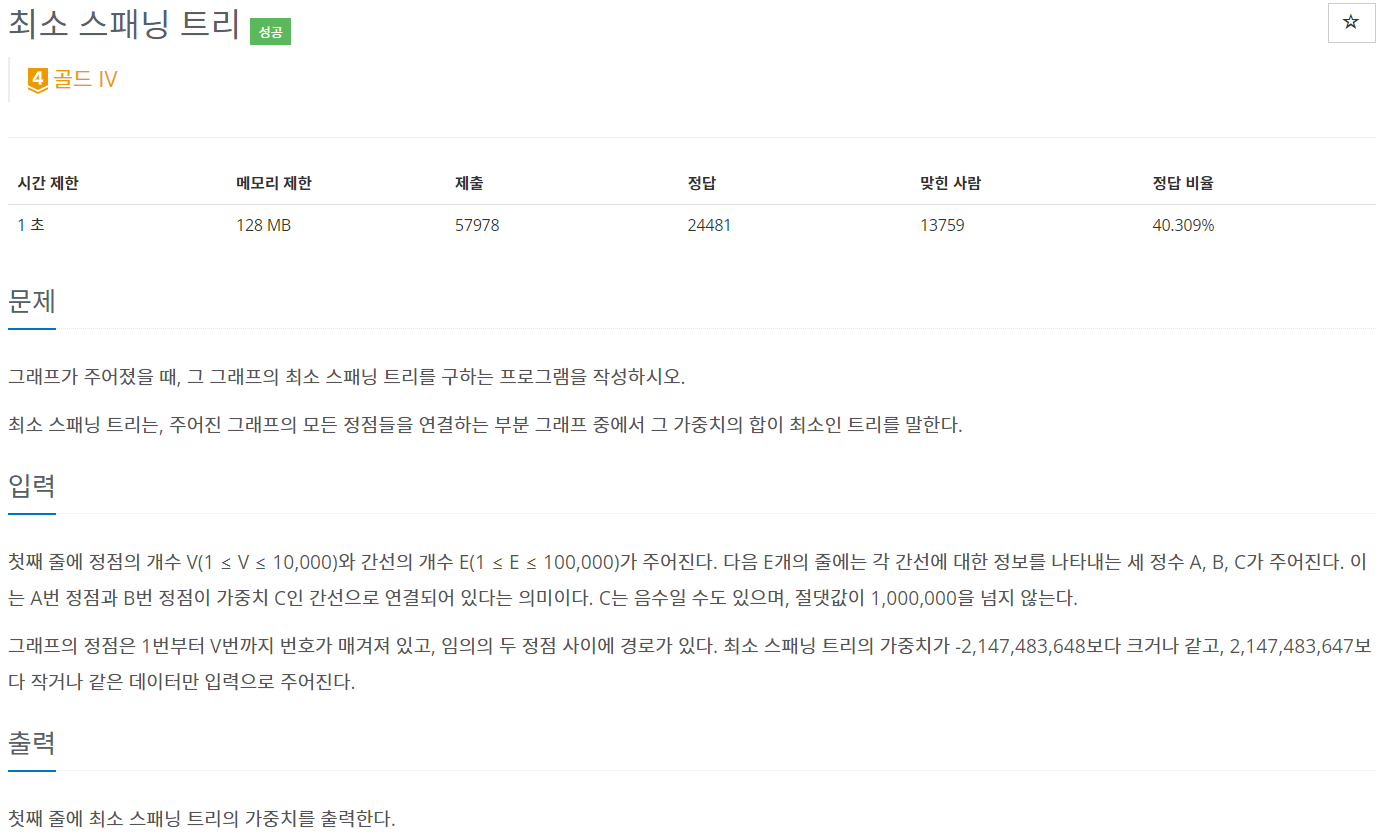
1197번: 최소 스패닝 트리
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이
www.acmicpc.net
풀이 1 - 크루스칼(Union & Find 활용)
최소 스패닝 트리를 구하는 알고리즘은 두 가지가 있다.
1. 크루스칼 (Union & Find 활용)
2. 프림 (PriorityQueue 활용)
크루스칼 알고리즘의 매커니즘
-> 크루스칼 알고리즘은 기본적으로 그리디한 선택을 바탕으로 알고리즘을 진행한다.
- 주어진 그래프의 모든 간선에 대해서, 간선의 연결비용을 낮은 순으로 오름 차순 정렬한다.
- 정렬된 간선 순서대로 선택하면서, 간선의 양 끝 정점을 Union 한다. 단, 이때 선택된 두 정점이 같은 집합에 속해있다면 사이클(cycle)이 있다고 판단하고 포함시키지 않는다.
이러한 매커니즘을 바탕으로 최종 선택된 간선을 연결한 것이 최소 비용 신장트리이다.
※ 크루스칼 알고리즘은 사실상 서로소 집합만 정확히 알고 있으면 매커니즘은 어렵지 않다. 서로소 집합에 대해서 먼저 명확히 이해하고 있어야만 한다.
간선 개수가 많을 경우
→ 트리가 완성되면 break
→ 최소 스패닝 트리의 edge 개수는 n-1
코드
import java.io.*;
import java.util.*;
public class Main {
static class Edge implements Comparable<Edge> {
int v1;
int v2;
int cost;
public Edge(int v1, int v2, int cost) {
this.v1 = v1;
this.v2 = v2;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
return this.cost - o.cost;
}
}
static int[] unf;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
unf = new int[n+1];
ArrayList<Edge> graph = new ArrayList<>();
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
graph.add(new Edge(a, b, c));
}
System.out.println(kruskal(graph, n));
}
static int kruskal(ArrayList<Edge> graph, int n) {
Collections.sort(graph);
for (int i = 1; i <= n; i++)
unf[i] = i;
int sum = 0;
for (Edge edge : graph) {
int fv1 = find(edge.v1);
int fv2 = find(edge.v2);
if (fv1 != fv2) {
sum += edge.cost;
union(edge.v1, edge.v2);
}
}
return sum;
}
static int find(int v) {
if (unf[v] == v) return v;
return unf[v] = find(unf[v]);
}
static void union(int v1, int v2) {
int fv1 = find(v1);
int fv2 = find(v2);
if (fv1 != fv2) unf[fv1] = fv2;
}
}
풀이 2 - 프림(PriorityQueue 활용)
프림 알고리즘은 최소 신장트리를 구하는 또 하나의 알고리즘으로, 하나의 시작 정점을 기준(보통 1부터 시작)으로 가장 작은 간선과 연결된 정점을 선택하여 스패닝 트리가 될 때까지 모든 노드를 연결시킨다. 따라서 항상 선택된 간선들은 중간 과정에서도 항상 연결된 트리를 이루게 된다.
임의의 정점에서 시작하여, 이미 만들어진 트리에 인접한 간섭만을 고려한다는 점을 제외하면 프림은 크루스칼과 완전히 똑같다. 프림 알고리즘 또한 선택할 수 있는 간선들 중 가중치가 가장 작은 간선을 선택하는 과정을 반복하기 때문이다.
코드
import java.io.*;
import java.util.*;
public class Main {
static class Edge implements Comparable<Edge> {
int vertex;
int cost;
public Edge(int vertex, int cost) {
this.vertex = vertex;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
return this.cost - o.cost;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
ArrayList<ArrayList<Edge>> graph = new ArrayList<>();
for (int i = 0; i <= n; i++)
graph.add(new ArrayList<>());
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
graph.get(a).add(new Edge(b, c));
graph.get(b).add(new Edge(a, c));
}
System.out.println(prim(graph, n));
}
static int prim(ArrayList<ArrayList<Edge>> graph, int n) {
PriorityQueue<Edge> pq= new PriorityQueue<>();
pq.add(new Edge(1, 0));
boolean[] visited = new boolean[n+1];
int sum = 0;
while (!pq.isEmpty()) {
Edge cur = pq.poll();
int vertex = cur.vertex;
if (visited[vertex]) continue;
visited[vertex] = true;
sum += cur.cost;
for (Edge e : graph.get(vertex)) {
if (!visited[e.vertex]) {
pq.add(e);
}
}
}
return sum;
}
}

Reference
'Algorithm 문제 풀이 > 백준' 카테고리의 다른 글
| [백준] 1991번 : 트리 순회 - 자바[Java] (0) | 2022.11.20 |
|---|---|
| [백준] 11725번 : 트리의 부모 찾기 - 자바[Java] (0) | 2022.11.20 |
| [백준] 13549번 : 숨바꼭질 3 - 자바[Java] (0) | 2022.11.19 |
| [백준] 1504번 : 특정한 최단 경로 - 자바[Java] (0) | 2022.11.19 |
| [백준] 1753번 : 최단경로(다익스트라) - 자바[Java] (0) | 2022.11.19 |
